紙ヒコーキCS-1のエンジンナセルその１

下図（CS-1）の 3D アニメ化を試みます。今回はエンジンナセル（ぐるぐる巻部分）を構成すべく、らせんの描画に取り組みます。例によって、動画とそのPythonソースコード（Google Colab ではない Python 開発環境が必要です。）を示します。動きがぎこちないので改善を検討します。2023.03.06 改善しました。

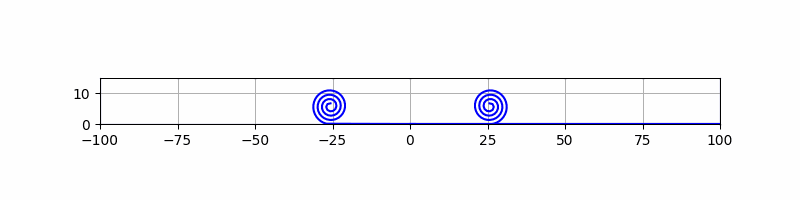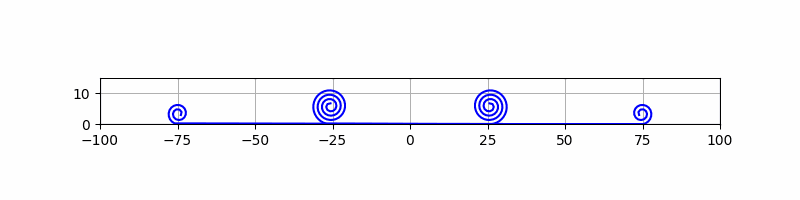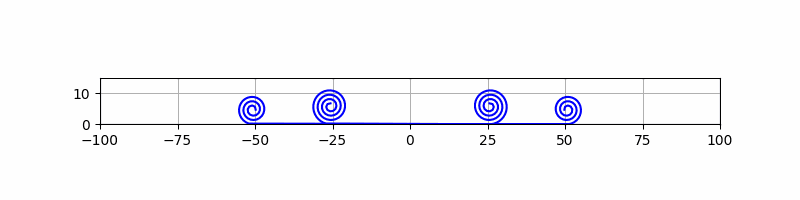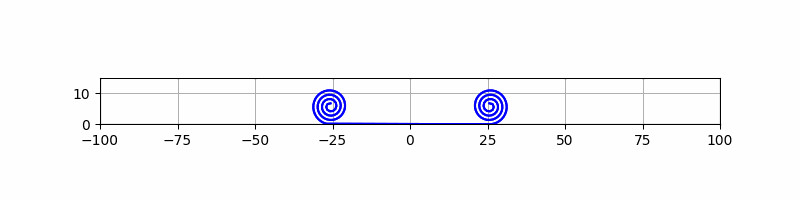
# CS-1-engine-1.py
# CS-1 螺旋部分２次元アニメ　　　2023.02.10 modified 2023.03.06 by Kero
# 回転角に比例してらせん中心からの距離が長くなる「等差らせん」を作る。
# 接線の傾きをらせんの回転角とする。
# 各点における接線の傾きは点iから点i-1の傾きとする。

import sys
import signal
import time
import datetime
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation

fig, ax = plt.subplots(figsize=(8.0, 2.0))
# fig, ax = plt.subplots()
ax.set_aspect('equal')
artists = []

ri = 1.0 # らせん中心と各点との距離。最初は100番目の点の値。
sp = 1 # 点間の距離
xi = np.linspace(0, 100, 101) # 各点のx座標の初期値。ゼロから100まで。
yi = [0.0] * 101 # 各点のｙ座標の初期値。すべてゼロ。
# y軸対称図形を作る。
xj = np.linspace(0, 100, 101)


do = [0.0] * 101 # do が何か分からない。03.06

# ＄＄＄＄　以下、何をしているのか分からない！　＄＄＄＄ 03.06

for i in range(100, -1, -1):
        do[i] = (np.pi/2 - np.arctan2(ri, 1)) * 1.5
        ri = np.sqrt(np.square(ri) + np.square(sp))

for eachx in range(101, 26, -1):
        for mag in range(100,eachx-1, -1):
                xsa = xi[mag] - xi[eachx-1]
                ysa = yi[mag]
                the = np.arctan2(ysa, xsa)
                kyo = np.sqrt(np.square(xsa) + np.square(ysa))
                kai = the + do[eachx -1]
                xi[mag] = xi[eachx-1] + kyo * np.cos(kai)
                xj[mag] = -xi[mag]
                yi[mag] = yi[eachx-1] + kyo * np.sin(kai)


        artist1 = ax.plot(xi,yi,"blue")
        artist2 = ax.plot(xj,yi,"blue")
        artists.append(artist1 + artist2) # こうすればスムーズに動く。
        
artist1 = ax.plot(xi,yi,"blue")
artist2 = ax.plot(xj,yi,"blue")

plt.xlim(-100, 100)
plt.ylim(0, 15)
ax.grid()
anim = ArtistAnimation(fig, artists, interval=10, repeat=True)

anim.save('engine1.gif', writer='pillow')
        
plt.show()
plt.close()
sys.exit()