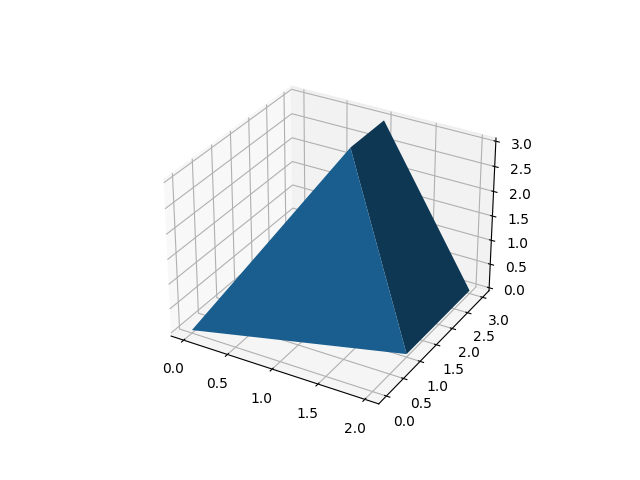
レッスン11 からの展開です。
ヨコに隣同士の2面をつなぎます。
# python-3D-graphics-step-by-step-12.py 10/04/2023 by Kero
# (12) show consecutive planes in 3D
# In a fig-window, you can change view point by mouse.
# Preparation
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# graph area settings
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# add a side plane (a bit complicated)
x = np.array([[1, 0],[1, 2],[1,2]]) # 2重リストの中身はxyzを縦に読む。2点で1線分。
y = np.array([[2, 0],[2, 1],[3,3]]) # 3本の線分を設定。1本目と2本目の線分で
z = np.array([[3, 0],[3, 0],[3,0]]) # 1面、2本目と3本目の線分でもう1面。
planes = ax.plot_surface(x, y, z) # 2つの線分が成す面を'surface'で描く。
# なお、線分間は平行でなくても良いが、平行でないと不思議な曲面になる。
fig.savefig('python-3D-graphics-step-by-step-12.png')
# show figure
plt.show()
レッスン11 では、線分(1, 2, 3)〜(0, 0, 0) と(1, 2, 3)〜(2, 1, 0) が成す面を描きました。
今回は、上記の線分(1, 2, 3)〜(2, 1, 0)を一辺とする面を追加します。
もう一辺(線分)は、(1, 3, 3)〜(2, 3, 0) です。16〜18行目の中に追記しています。
要するに、線分を構成する2点の座標を一組にして、x, y, z 配列に[ ]で加えれば、次から次とヨコ隣の面ができます。

