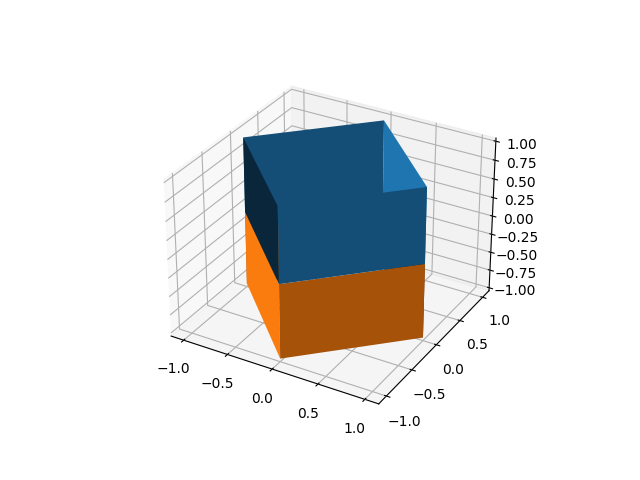
最初にレッスン13のような「四角筒」を作ります。ただし、上のフタは作りません。また、レッスン13では側面がx軸またはy軸に平行でしたが、今回は 45° ずれています。
なぜこのようなモノを作るの?
それは、今回の四角筒の作り方を応用して、n角筒や円筒を作るためです。
# python-3D-graphics-step-by-step-15.py 12/04/2023 by Kero
# (15) show a cylinder in 3D
# Preparation
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
pi = np.pi # π=3.14... を'pi'に代入。
# graph area settings
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# make figures
# (1) 角張った円筒(4角筒)
keido = np.array([0, 0.5*pi, np.pi, 1.5*pi, 2*pi]) # ---(1) 1周を4等分。
x = np.cos(keido) # xもkeidoと同じndarray(数値配列型)になる。
y = np.sin(keido) # yもndarrayになる。
x1 = np.array([[x[0],x[0]],[x[1],x[1]],[x[2],x[2]],[x[3],x[3]],[x[4],x[4]]])
y1 = np.array([[y[0],y[0]],[y[1],y[1]],[y[2],y[2]],[y[3],y[3]],[y[4],y[4]]])
z1 = np.array([[0, 1],[0, 1],[0, 1],[0, 1],[0, 1]])
# [x[0],x[0]]等は単なるリストだから、それぞれ改めて'np.array'で数値配列型にする。
walls1 = ax.plot_surface(x1, y1, z1)
# (2) ほぼ円筒(角数 = kaku)
kaku = 4 # カク数。後でもっと大きな整数に変更してみてください。
keido = np.linspace(0, 2*pi, kaku+1) # ---kaku=4の場合、式(1)と同じ。
x = np.cos(keido) # xもndarray(配列)になる。
y = np.sin(keido) # yもndarray(配列)になる。
z = [0,-1] # z は'ndarray'ではなく、「リスト」。
x2 = [] # 外側のリスト型を用意。
y2 = []
z2 = []
for i in range(kaku+1):
x2.append([x[i],x[i]]) # x2は「リストのリスト」。
y2.append([y[i],y[i]]) # y2も「リストのリスト」。
z2.append(z) # 同じく「リストのリスト」。
x2n = np.array(x2) # x2をndarray(数値配列型)に変換。
y2n = np.array(y2) # 同上。
z2n = np.array(z2) # 同上。
walls2 = ax.plot_surface(x2n, y2n, z2n)
fig.savefig('python-3D-graphics-step-by-step-15.png')
# show figure
plt.show()
graph area setting までレッスン12と同じです。
「make figures」では、地球や世界地図に出てくる「緯度(いど)と経度(けいど)」の「経度」を使って考えます。「 (1) カクばった円筒(4角筒)」では、「経度」として、0、π/2、π、3π/2、2π の数値配列(np.array)を設定しています。xy 軸平面上の半径 = 1 の円を想定し、それをz軸の上の方から見ます。上記の経度の数値配列に対応する円周上の点のxy座標は、x=cos(経度)及びy=sin(経度)の式から、それぞれ (1, 0), (0,1), (-1,0), (0,-1), (1, 0) になります。x 座標だけ集めて17行目の x(数値配列)ができます。18行目の y も同様です。
それぞれの点を通る z軸に平行な長さ1の線分(xy軸平面から上に1だけ伸びています)は、例えば最初の線分は (1,0,0)〜(1,0,1) です(以下同文)。レッスン13で平面を作ったように、20行目から22行目で線分を並べています。これらは数値配列型にする必要があります。
walls1 で上側の四角筒を作ります。
「(2) ほぼ円筒(角数 = kaku)」では、「経度」の数を変更できるようにしています。
29行目の “np.linspace” は、引数1 から引数2 までを 「引数3 – 1」等分し、数値配列型にします。
38行目の “for i in range(n):” は、以下のインデントした段落で、i が 0 から n-1 になるまで繰り返します。例えば39行目では、2点からなる線分のx 座標をリストにして リスト x2 に追加しています。y2 と z2 も同様です。ただこれらの「リストのリスト」は数値型ではないので43〜45行目で数値配列型に変換しています。
後はこれまで同様です。

