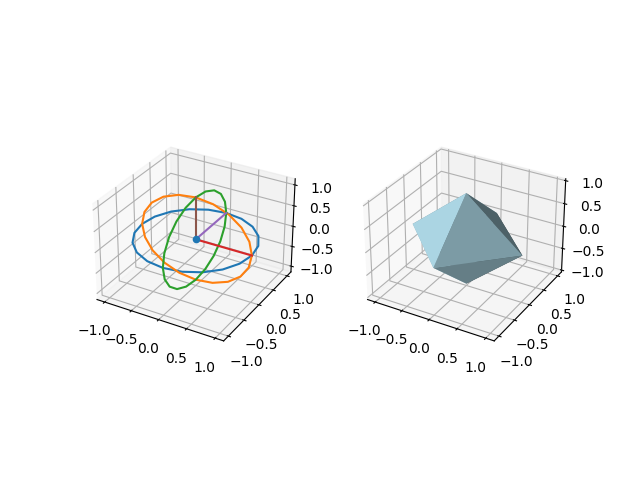
このレッスンが本講座の「ヤマ場」です。中身はレッスン14と15の応用です。
地球の「緯度と経度」を意識して、角張ったコマみたいな多面体を作ります。
まず、多面体を作る理解のための球体上の補助線図(左図)を作り、その次にコマ(右図)を作ります。
多面体を「球」にするには、各自でパラメータを変更して試してみてください。
# python-3D-graphics-step-by-step-16.py 13/04/2023 by Kero
# (16) show a ball in 3D
# You can endure a difficulty of drawing a ball-like figure.
# Get through it with a fight!
# Preparation
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
pi = np.pi
# graph area settings
fig = plt.figure()
ax1 = fig.add_subplot(121, projection='3d')
ax2 = fig.add_subplot(122, projection='3d') # ガクブチを2つ用意します。
# make auxiliary lines
# 球体の作画を理解するための補助線図をガクブチ「ax1」に作ります。
kado = 20
en = np.linspace(0, 2*pi, kado+1) # 円周を20等分。21等分ではありません。
a1 = np.cos(en) # 各en値の'cos'の「リスト」ができます。
a2 = np.sin(en) # 各en値の'sin'の「リスト」ができます。
a3 = [0]*(kado+1) # [0, 0, 0, ..., 0] のリスト(0が21個)ができます。
f1 = ax1.plot(a1,a2,a3) # z=0平面(xy平面)に円ができます。ガクブチ「ax1」の中です。
f2 = ax1.plot(a2,a3,a1) # y=0平面(zx平面)に円ができます。
f3 = ax1.plot(a3,a1,a2) # x=0平面(yz平面)に円ができます。
ce = ax1.scatter(0,0,0) # 中心の原点表示。
l1 = ax1.plot([0,1],[0,0],[0,0]) # 原点とx軸上の交点を結びます。
l2 = ax1.plot([0,0],[0,1],[0,0]) # 原点とy軸上の交点を結びます。
l3 = ax1.plot([0,0],[0,0],[0,1]) # 原点とz軸上の交点を結びます。
# make a ball-like figure
# ここでは角張った球(八面体)をガクブチ「ax2」に描きます。
# 「たとえ」として「地球」を考えます。
# 地球上のある地点を示すためには「経度と緯度」を用います。
# 経度とは、地球上の「ある地点」と北極を結ぶ線で地球を縦斬りにしたとき、その切り口が、
# 「基準となるグリニッジ天文台」の切り口と何度違うか、という「角度」のことです。
# ここでは、経度キザミは赤道1周を4等分した角度の、
# 0, π/2, π, 3π/2, 2π (最後の2πはゼロと同等)とします。
# 緯度とは「ある点」の「仰角」のことですが、「幾何学における極座標」にならって、
# ここでは、z軸の正方向(北極方向)からの傾き角度とします。
keido = np.array([0, pi/2, pi, 3*pi/2, 2*pi]) # 経度キザミ(角度)です。赤道面を4等分しました。
# = np.linspace(0, 2*pi, 5) と同じ。リスト内の値を、k0,k1,k2,k3,k4とします。
ido = np.array([0, pi/2, pi]) # 緯度キザミ(角度)です。
# = np.linspace(0, pi, 3) と同じ。リスト内の値を、i0,i1,i2とします。
# 角度と半径(=1)の極座標から経度・緯度の各交点のxyz座標を求めます。
# ①まず緯度zのところにある水平円の半径を求めます。→ sin(ido)
# ②その水平円と経度が交差する点のx座標を求めます。→ cos(keido)*sin(ido)
# ③y座標は、→ sin(keido)*sin(ido)
# ④z座標は、→ cos(ido)
# まとめると、ある経度(例えば=0)に沿った各緯度(=0, π/2, π)との交点のx座標3つは、
# [cos(k0)*sin(i0), cos(k0)*sin(i1), cos(k0)*sin(i2)]
# = [0, 1, 0]。
# 同様にして、y座標3つは、
# [sin(k0)*sin(i0), sin(k0)*sin(i1), sin(k0)*sin(i2)]
# = [0, 0, 0]
# z座標3つは、
# [cos(i0), cos(i1), cos(i2)]
# = [1, 0, -1]
# 各リストを縦に並べて、列ごとに読むと、xyz座標=(0,0,1),(1,0,0),(0,0,-1)が、
# keido=0 における折れ線の各頂点になっていることが分かります。
# x座標について、経度[k0,k1,k2,k3,k4]と緯度[i0,i1,i2]を掛け合わせて、以下のリストを作る必要があります。
# [[cos(k0)*sin(i0),cos(k0)*sin(i1),cos(k0)*sin(i2)],
# [cos(k1)*sin(i0),cos(k1)*sin(i1),cos(k1)*sin(i2)],
# [cos(k2)*sin(i0),cos(k2)*sin(i1),cos(k2)*sin(i2)],
# [cos(k3)*sin(i0),cos(k3)*sin(i1),cos(k3)*sin(i2)],
# [cos(k4)*sin(i0),cos(k4)*sin(i1),cos(k4)*sin(i2)]]
# y座標も同様。(cos(k)がsin(k)に変わります。)
# z座標は、[cos(i0),cos(i1),cos(i2)] = [1, 0, -1]の繰り返しで「リストのリスト」を作ります。
# x,y,z座標の各作業をそれぞれ1発で処理する関数があります。
# ベクトルの外積(正しくはテンソル積)を計算する'np.outer()'です。
# 'np.outer()'は、例えば[a0,a1,a2]と[b0,b1]について、すべての要素を掛け合わせて、
# [[a0b0,a0b1],[a1b0,a1b1],[a2b0,a2b1]]を出力してくれます。よって、
x = np.outer(np.cos(keido), np.sin(ido))
y = np.outer(np.sin(keido), np.sin(ido))
z = np.outer(np.ones(np.size(keido)),np.cos(ido))
# なお、'np.ones(np.size(keido))'は、keidoの要素数分'1'を持つリストを作れ、という命令です。
ball = ax2.plot_surface(x, y, z, color='lightblue') # ガクブチ「ax2」の中に八面体を作ります。
fig.savefig('python-3D-graphics-step-by-step-16.png') # fig(壁面)単位でセーブします。
plt.show()
辛抱してチャレンジしましょう。
15行目と16行目で、2つのガクブチを用意しました。
18行目の “make auxiliary lines” から31行目までは、球の作画を理解するための補助線を描くコードです。
29行目の l1 は (0, 0, 0)から(1, 0, 0) までの線分です。以下同様です。
詳しくは、ソースコードのコメント文をお読みください。
次の33行目からが本番です。
keido(経度)の数値配列型リストはレッスン15の上の四角筒の設定と同一ですが、角形数を増やす場合は “np.linspace” を使ってください。コメント文の中では0=k0, π/2=k1, π=k2, 3π/2=k3, 2π=k4 としています。同様にしてido(緯度)も、角形数を増やす場合は “np.linspace” を使ってください。コメント文では 0=i0, π/2=i1, π=i2 としています。
設定した各経度と緯度が交わるところの点を結んで「多面体」を作ります。
南極点と北極点を結ぶ4つの「経線」は、設定した緯度との交点で折れ曲がる「折れ線」になっていています。レッスン14を思い出してください。ここでも同様に、折れ線の中の「上端点」と「折れ点」と「下端点」を順番に並べて x,y,z の各座標値ごとに「リスト」にし、それらを経線(レッスン14では「稜線」)ごとにヨコに並べて「リストのリスト」を作ります。実際の座標の数値の算出原理は、コードの47行目から63行目のコメントに書いています。
64行目以降で、同様にして全ての経度と全ての緯度の全交点の x,y,z 座標の値を算出します。うひゃー! 大変だ! でも恐れないでください。
65行目から69行目を見てください。規則性があります。例えば x の値については、左縦に cos(各経度) の値を並べ、上横に sin(各緯度)を並べた表を作り、タテ・ヨコ掛け算して表を埋めるという方法で、計算できます。numpyにはそれを一発で処理する関数があります。73行目で紹介する “np.outer()” です。この関数の本来的な使い道は線形代数分野だそうですが、ちょうど今回の計算にピッタリです。
76行目はこのままで65〜69行目の「数値配列型リストのリスト」ができます。78行目の z はちょっと応用ですが、79行目に説明したとおりです。
81行目で描画される多面体は、各稜の長さが全て√2 の正八面体です。44行目と46行目の角数(5とか3)を増やして、多面体がどうなるかお試しください。ただし、増やすとその分だけ計算が遅くなります。
なお、どちらの図もマウスの左クリックでグリグリ動きます。

