# makizushi-01.py 2023.03.22 by Kero
# 最終目標は「巻きずしを作る3Dアニメ」です。
# 簡単なところから少しずつプログラムを作り込んでいきます。
# PCでは「らせん」やその他の曲線は、点と点を直線でつないで作ります。
# 「代数らせん(アルキメデスのらせん)」の公式を使います。
# 1. 2次元静止画「代数らせん」作り (makizushi-01.py)
# (1) 必要なモジュールをインポート。
import sys
import numpy as np
import matplotlib.pyplot as plt
pi = np.pi # π(パイ)をpiとしておきます。
# (2) 公式から「代数らせん」の座標を計算。
# 「代数らせん」の公式は、r = a・θ です。(r:らせん半径。θ:回転角度。)
# 1周(⊿θ=2π)ごとの線間距離を a にしたいので、公式を「r = a・θ/2π」とします。
# 巻き始め点が、らせん中心から r0 だけ離れていることとします。
# r0 = a・θ/2π となる θ をθ0とし、巻き始め点は既にθ0だけ巻いていると考えます。
# 巻き始め点から「らせん」を伸ばし、ちょうど1周(2π)したところの先端点は、
# 巻き始め点から a だけ離れています。1周目と2周目、n周目とn+1周目も同じです。
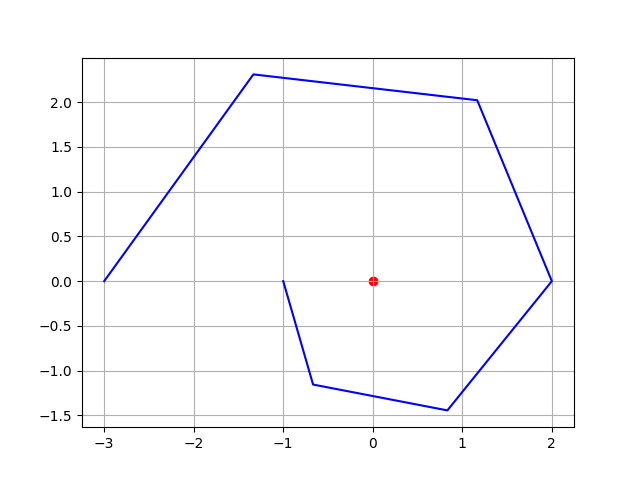
# ちなみに、巻数は1周、r0=1、a=2 のらせんを描いてみます。
maki = 1
r0 = 1
a = 2
# 巻き始め点は既に kaku0 だけ巻いていると考えると。
kaku0 = 2 * pi * r0 / a
# これから巻数分だけ巻いていきます。
# 「絵の粗さ」を設定します。点と点の間隔とか、らせん中心における点間の角度です。
# ここでは、らせん中心における点間の角度が1周の何等分か、で絵の粗さを設定します。
ara = 6 # ちなみに、粗さ(ara)を1周の6等分とします。
pon = maki * ara + 1 # 座標点の数です。
# らせんを描く各点の、巻き始め点からの角度を設定します。
# ゼロから始まり 2π*maki まで、2π/ara ごとに加算された回転角の配列(kaku)を作ります。
kaku = np.linspace(0, 2 * pi * maki, pon)
# 最後の +1 はゼロも含むためです。
# 巻き始め点までの仮想回転角とそれ以降の回転角を合わせた角度を kakut とします。
kakut = kaku + kaku0 # 配列kakuの各要素に定数kaku0が加算されkakutに収納。
# r は何回も出てくるので、計算しておきます。公式(改変済)より、
r = a * kakut / (2 * pi) # kakutが配列なのでrも配列。
# rとθの極座標パラメータから、xy座標に変換します。
x = r * np.cos(kakut)
y = r * np.sin(kakut)
# (3) グラフ作成。
fig, ax = plt.subplots() # グラフ領域を用意。
ax.set_aspect('equal') # タテヨコ同じ目盛りにします。
ax.grid() # グリッド(碁盤の目)を表示します。
ax.scatter(0,0,c='r') # らせん中心点を赤丸で書き込み。
ax.plot(x, y, c='b') # らせんを青線で書き込み。
plt.show() # グラフ表示。
plt.close() # グラフおわり。
sys.exit() # 処理おわり。
# パラメータを変えて試行してみてください。